Si consideri il seguente grafo:
La matrice delle adiacenze è
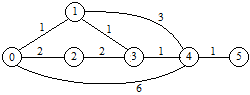
Ricerca del cammino minimo dal nodo i al nodo j su un grafo pesato (con pesi≥0).
Il grafo è rappresentato tramite la matrice delle adiacenze e i nodi sono indicati con un numero intero da 0 a n-1.
n: numero dei nodi che compongono il grafo.
matrice delle adiacenze g. È una matrice di nxn interi
vettore delle distanze. È un vettore di n interi. Per ciascun nodo contiene la minima distanza dal nodo di partenza. Ad ogni elemento viene assegnato il valore iniziale INT_MAX, per indicare che il nodo non è ancora stato raggiunto da nessun possibile percorso
vettore delle provenienze. È un vettore di n interi. Per ciascun nodo contiene il numero del nodo che lo precede nel cammino minimo. Ad ogni elemento viene assegnato il valore iniziale -1, per significare che non è stato ancora raggiunto da un possibile percorso.
vettore dei nodi visitati. È un vettore di n booleani (o interi). Ad ogni elemento viene assegnato il valore iniziale 0 (Falso, non visitato), successivamente, assumerà il valore 1 (Vero, visitato) quando verrà preso in considerazione per stabilire se appartiene ad un persorso di costo minimo.
i e j indice di riga e indice di colonna per la matrice delle adiacenze.
nodoAttuale. È una variabile intera che indica il nodo in esame. Come valore iniziale le viene assegnato il numero del nodo di partenza.
inizio è il numero del nodo di partenza, fine è il numero del nodo di arrivo. Sono due variabili intere il cui valore viene fornito in input.
minDistanza è un intero usato per cercare la distanza minima dopo aver esaminato tutti i costi dei percorsi per raggiungere un nodo successore.
nodoAttuale ← inizio
visitato[nodoAttuale] ← 1
distanza[inizio] ← 0
minDistanza = 0
finchè (nodoAttuale diverso da fine) e (ci sono ancora nodi raggiungibili)
per tutti i nodi j
Aggiungi al costo del cammino percorso, il costo tra il nodoAttuale e il nodo j
se il costo ottenuto è minore del costo per raggiungere i
sostituisci il costo (distanza[j]) con il costo tra ila nodoAttuale e il percorso verso j
aggiorna il nodo di provenienza
Scelta del nodo a cui si è giunti con un percorso di costo minimo nodo e che non sia ancora stato visitato
(questo diventa nodoAttuale).
il nodo scelto diventa nodoAttuale. Non dovrà essere riesaminato, quindi lo si marca come visitato
fine finchè
#include <cstdlib>
#include <iostream>
#include <fstream>
#include <climits>
using namespace std;
int main() {
/*
Dichiarazioni delle variabili intere
*/
I dati verranno forniti nel file di testo "input.txt" e i risultati verranno registrati nel file di testo "output.txt".
Dichiarare i due file: in e out:
ifstream in("input.txt");
ofstream out("output.txt");
Il file input.txt contiene:
nella prima riga 3 interi:
il numero dei nodi che compongono il grafo,
il numero del nodo di partenza,
il numero del nodo di arrivo
nelle righe successive contiene le terne che consentono di costruire la matrice delle adiacenze:
nodo i,
nodo j adiacente ad i
costo del cammino da i a j
I nodi sono numerati a partire da zero allo scopo di metterli in corrispondenza con gli indici dei vettori
Lettura della prima riga del file:
int n; //numero dei nodi in >> n; // numero dei nodi in >> inizio; // nodo di partenza in >> fine; // nodo di arrivo
Per verifica, viene preparato un messaggio nel file di output:
out << n << " nodi" << endl; // messaggio di output out << "ricerca del percorso di costo minimo da " << inizio << " a " << fine << endl;
Dichiarazione della matrice delle adiacenze:
int **g; // g è un array di puntatori a puntatori int
g = new int *[n]; // assegna a g l'indirizzo di un array di n puntatori a int
for (k=0; k<n; k++)
g[k] = new int[n]; // ad ognuno degli n puntatori assegna l'indirizzo di un array di n int
Prima di assegnare i costi tra i nodi adiacenti, si assume che tra tutti i nodi i e j non ci sia un percorso. Si assegna il valore predefinito INT_MAX ad ogni elemento della matrice delle adiacenze.
for (i=0; i<n; i++)
for (j=0; j<n; j++)
g[i][j] = INT_MAX;
Dal file di input vengono lette le righe contenenti una coppia di nodi e il costo del cammino tra essi
while (!in.eof()) {
in >> i; // lettura del numero del nodo
in >> j; // lettura di un successore del nodo i
in >> g[i][j]; // costo del cammino da i a j
}
in.close();
distanze è un puntatore a int creare un array di n int ed assegnare il suo indirizzo a distanze provenienze è un puntatore a int creare un array di n int ed assegnare il suo indirizzo a provenienze visitato è un puntatore a int creare un array di n int ed assegnare il suo indirizzo a visitato
Un elemento j del vettore distanze è associato ad un nodo j, questo elemento rappresenta la minima distanza del nodo j dal nodo di partenza.
for (i=0; i<n; i++)
distanze[i] = INT_MAX;
L'assegnazione del valore INT_MAX ad un nodo serve per specficare che il nodo non risulta ancora adiacente a nessuno dei nodi visitati.
Un elemento j del vettore provenienze specifica qual è il nodo precedente lungo il cammino di costo minimo. Il valore iniziale di ogni elemento dell'array è -1 per indicare che il nodo non è stato ancora raggiunto.
for (i=0; i<n; i++)
provenienze[i] = -1;
L'array visitato è un vettore di booleani. Per ciascun nodo specifica 0 se non visitato, 1 se visitato
for (i=0; i<n; i++)
visitato[i] = 0;
Il cammino inizia dal nodo inizio e il costo di questo primo passo è 0.
nodoAttuale= inizio; distanze[inizio] = minDistanza = 0; // anche il costo del cammino è 0
Tra tutti i successori del nodoAttuale si cerca quello non ancora visitato ed avente il minimo costo:
while (nodoAttuale != fine && minDistanza != INT_MAX) {
minDistanza = INT_MAX;
for (j=0; j<n; j++)
if (!visitato[j] && distanze[j] < minDistanza) {
minDistanza = distanze[j];
nodoAttuale = j;
}
A questo punto si è trovato il nodo a cui si giunge con il minimo costo. Viene scelto per proseguire il cammino.
Il nodo scelto viene marcato come visitato per non essere più considerato
visitato[nodoAttuale] = 1;
valutazione dei costi tra tutti i successori del nodo attuale e aggiornamento dei costi dei cammini:
for (j=0; j<n; j++)
if (g[nodoAttuale][j] != INT_MAX
&&
distanze[j] > distanze[nodoAttuale] + g[nodoAttuale][j]
) {
distanze[j] = distanze[nodoAttuale] + g[nodoAttuale][j];
provenienze[j] = nodoAttuale;
}
}
stampa dei risultati:
if (!visitato[fine])
out << "non esiste cammino da nodo " << inizio << " a " << fine << endl;
else {
out << "cammino di costo " << distanze[fine];
i = fine;
out << endl << "percorso a ritroso: ";
while (i != inizio) {
out << i << " ";
i = provenienze[i];
}
out << i << " ";
}
out.close();
return EXIT_SUCCESS;
}
il file input.txt
6 1 5 1 2 5 2 3 1 3 4 3 4 5 2 5 1 6 1 4 4
il file prodotto in output:
6 nodi ricerca del percorso di costo minimo da 1 a 5 cammino di costo 6 percorso a ritroso: 5 4 1
Modificare i costi e verificare che viene scelto il percorso di costo minimo.
introdurre la matrice delle adiacenze di un grafo più complesso
Associare un nome ad ogni numero di nodo e e stampare il percorso di costo minimo specificando i nomi anzichè i numeri dei nodi.
Si consideri il seguente grafo: |
La matrice delle adiacenze è |
||||||
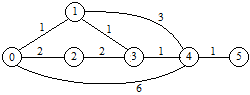 |
0 | 1 | 2 | 3 | 4 | 5 | |
| 0 | 0 | 1 | 2 | ∞ | 6 | ∞ | |
| 1 | ∞ | 0 | ∞ | 1 | 3 | ∞ | |
| 2 | ∞ | ∞ | 0 | 2 | ∞ | ∞ | |
| 3 | ∞ | ∞ | ∞ | 0 | 1 | ∞ | |
| 4 | ∞ | ∞ | ∞ | ∞ | 0 | 1 | |
| 5 | ∞ | ∞ | ∞ | ∞ | ∞ | 0 | |
nodoAttuale = minDistanza = 0 distanza[nodoAttuale] = 0
Vettore distanze:
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| costo da Nodo Iniziale | 0 | ∞ | ∞ | ∞ | ∞ | ∞ |
Un elemento j del vettore distanze rappresenta la minima distanza del nodo j dal nodo inizio.
Vettore Provenienze
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| precedente: | -1 | -1 | -1 | -1 | -1 | -1 |
Un elemento j del vettore provenienze specifica il nodo precedente lungo il cammino di costo minimo. Il valore -1 significa provenienza sconosciuta
Vettore Visitato
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| visitato: | 0 | 0 | 0 | 0 | 0 | 0 |
Per ciascun nodo 0 indica nodo non visitato, 1 indica nodo visitato.
while (nodoAttuale!=fine) {
La condizione specificata è soddisfatta: il nodo attuale 0 è diverso dal nodo di arrivo 5, quindi si entra nel ciclo.
Ciclo di ricerca del minimo in un vettore:
Si cerca il nodo non ancora visitato ed avente costo minimo dal nodo di partenza.
minDistanza=INT_MAX;
for (i=0; i<n; i++)
if (!visitato[i] && distanze[i] < minDistanza ){
minDistanza = distanze[i];
nodoAttuale=i;
}
visitato[nodoAttuale]=1;
Il nodo 0 diventa nodoAttuale. Viene marcato come visitato (per non esaminarlo più) e si aggiorna la variabile minDistanza.
Vettore Visitato
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| visitato: | 1 | 0 | 0 | 0 | 0 | 0 |
per tutte le possibili destinazioni del nodo 0 Calcola il costo del cammino ed aggiorna la provenienza.
Si esaminano tutti i valori della riga 0 della matrice delle adiacenze.
Solo per i nodi adiacenti al nodo 0 si aggiorna il vettore delle distanze, a condizione che si trovi un cammino più conveniente di quello già trovato e si aggiorna anche la provenienza.
for (i=0; i<n; i++)
if ( g[nodoAttuale][i]!=INT_MAX && distanze[i] > distanze[nodoAttuale] + g[nodoAttuale][i]) {
distanze[i] = distanze[nodoAttuale] + g[nodoAttuale][i];
provenienze[i]=nodoAttuale;
}
Vettore distanze:
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| costo dal Nodo Iniziale | 0 | 1 | 2 | ∞ | 6 | ∞ |
Vettore Provenienze
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| precedente: | -1 | 0 | 0 | -1 | 0 | -1 |
Si cerca il nodo non ancora visitato ed avente costo minimo dal nodo di partenza.
il nodoAttuale è 0 diverso da 5 (nodo di arrivo). Nel vettore distanze si cerca il nodo non ancora visitato ed avente il minimo costo. Si trova il nodo 1, che diventa nodoAttuale e viene marcato come visitato.
Vettore Visitato
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| visitato: | 1 | 1 | 0 | 0 | 0 | 0 |
Sulla riga 1 della matrice delle adiacenze si cerca la colonna j avente distanza minore.
per tutte le possibili destinazioni del nodo 1 Calcola il costo del cammino ed aggiorna la provenienza
Vettore distanze:
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| costo dal Nodo Iniziale | 0 | 1 | 2 | 2 | 4 | ∞ |
Vettore Provenienze
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| precedente: | -1 | 0 | 0 | 1 | 1 | -1 |
Si cerca il nodo non ancora visitato ed avente costo minimo dal nodo di partenza.
il nodoAttuale è 1 diverso da 5 (nodo di arrivo). Nel vettore distanze si cerca il nodo non ancora visitato ed avente il minimo costo. Si trova il nodo 2, che diventa nodoAttuale e viene marcato come visitato.
Vettore Visitato
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| visitato: | 1 | 1 | 1 | 0 | 0 | 0 |
Nella matrice delle adiacenze si valutano tutte le possibili destinazioni raggiungibili dal nodo 2. Si vede che si raggiunge il nodo 3 con costo 4, mentre il vettore distanze indica che lo stesso nodo 3 è stato già raggiunto con costo 2, quindi in questo ciclo il vettore distanze e il vettore provenienza non vengono aggiornati.
Si cerca il nodo non ancora visitato ed avente costo minimo dal nodo di partenza.
il nodoAttuale è 2 diverso da 5 (nodo di arrivo). Nel vettore distanze si cerca il nodo non ancora visitato ed avente il minimo costo. Si trova il nodo 3, che diventa nodoAttuale e viene marcato come visitato.
Vettore Visitato
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| visitato: | 1 | 1 | 1 | 1 | 0 | 0 |
Vettore distanze:
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| costo dal Nodo Iniziale | 0 | 1 | 2 | 2 | 3 | ∞ |
Un elemento j del vettore distanze rappresenta la minima distanza del nodo j dal nodo inizio.
Vettore Provenienze
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| precedente: | -1 | 0 | 0 | 1 | 3 | -1 |
Si cerca il nodo non ancora visitato ed avente costo minimo dal nodo di partenza.
il nodoAttuale è 3 diverso da 5 (nodo di arrivo). Nel vettore distanze si cerca il nodo non ancora visitato ed avente il minimo costo. Si trova il nodo 4, che diventa nodoAttuale e viene marcato come visitato.
Vettore Visitato
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| visitato: | 1 | 1 | 1 | 1 | 1 | 0 |
Per tutte le possibili destinazioni del nodo 4 si calcola il costo del cammino e si aggiorna la provenienza.
Vettore distanze:
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| costo dal Nodo Iniziale | 0 | 1 | 2 | 2 | 3 | 4 |
Un elemento j del vettore distanze rappresenta la minima distanza del nodo j dal nodo inizio.
Vettore Provenienze
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| precedente: | -1 | 0 | 0 | 1 | 3 | 4 |
Si cerca il nodo non ancora visitato ed avente costo minimo dal nodo di partenza.
il nodoAttuale è 4 diverso da 5 (nodo di arrivo). Nel vettore distanze si cerca il nodo non ancora visitato ed avente il minimo costo. Si trova il nodo 5, che diventa nodoAttuale e viene marcato come visitato.
Vettore Visitato
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| visitato: | 1 | 1 | 1 | 1 | 1 | 1 |
Per tutte le possibili destinazioni del nodo 5 si calcola il costo del cammino e si aggiorna la provenienza.
Vettore distanze:
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| costo dal Nodo Iniziale | 0 | 1 | 2 | 2 | 3 | 4 |
Vettore Provenienze
| Nodo Numero: | 0 | 1 | 2 | 3 | 4 | 5 |
| precedente: | -1 | 0 | 0 | 1 | 3 | 4 |
A questo punto il nodo Attuale è uguale al nodo di arrivo e il ciclo non viene ripetuto. A iniziare dal nodo di arrivo, si cerca nel vettore delle provenienze la successione di nodi da attraversare per percorrere il cammino di costo minimo.
Risultati:
cammino di costo 4
percorso a ritroso rilevato dal vettore delle provenienze: 5 4 3 1 0