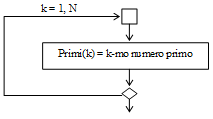
facendo assumere in successione alla variabile k i valori 1, 2, …, N, ripeti:
Primi[k] = k-mo numero primo
(memorizza nella posizione k dell'array Primi il k-mo numero primo)
da: "Programmazione dei calcolatori elettronici" - B. Fadini - Liguori - Napoli 1977
Per individuare il procedimento risolutivo di un problema si suggerisce di adottare la metodologia del raffinamento successivo (step-wise refinement oppure programmazione top-down). Questa si basa sui seguenti principi:
Si ammette che un programma sia costituito da segmenti e che ciascun segmento sia una delle strutture fondamentali della programmazione, non escludendo che ciascun blocco di tali strutture possa essere ancora una struttura.
Un problema può pertanto essere descritto a diversi livelli di sinteticità (o di astrazione), di questi il più sintetico (o il più astratto) descrive le specifiche funzionali del programma mediante le quali si individua che cosa fa il programma.
Un successivo livello di astrazione consiste nel descrivere come tali specifiche vengono implementate mediante una sequenza di azioni elaborative componenti collegate fra loro in una delle strutture fondamentali della programmazione. Tali azioni non sono in generale esprimibili direttamente in una frase del linguaggio di programmazione prescelto, ma sono ancora espresse in un linguaggio di astrazione che definisce che cosa ciascuna di esse fa.
Il procedimento si sviluppa iterativamente fino a pervenire al massimo livello di dettaglio (minimo livello di astrazione) che costituisce il cosiddetto programma concreto.
In altri termini si procede come se in ciascun livello di astrazione si disponesse di una macchina virtuale specializzata e costruita ad hoc per quel problema e quel livello di astrazione, nella quale siano definite le strutture dati e le operazioni necessarie alla risoluzione del problema: lo sforzo della progettazione consiste pertanto, per ciascun livello, nella precisa identificazione delle azioni elaborative e dei dati su cui esse operano. Per ciascuna delle azioni elaborative cosi individuate, il processo di raffinamento può considerarsi terminato nelle ipotesi che esse siano definite nel linguaggio di programmazione prescelto oppure siano disponibili attraverso l'impiego di sottoprogrammi; in caso contrario l'azione elaborativa deve essere raffinata finchè non sia verificata la condizione di termine del raffinamento.
Nel processo di raffinamento vengono via via dettagliati da un lato l'algoritmo di calcolo, dall'altro le strutture dati.
La tendenza della programmazione strutturata è quella di non anticipare decisioni che non siano strettamente necessarie al livello di astrazione in cui si opera, in quanto ogni decisione di dettaglio anticipata, da un lato distrae l'attenzione sullo sviluppo di quel livello, e dall'altro potrebbe essere incompatibile con lo sviluppo dei livelli successivi. D'altro canto, va anche considerato che - come in tutte le progettazioni tecniche - il processo di progettazione di un programma non si può circoscrivere in una metodologia che proceda in forma rigida e che non preveda le intuizioni e i ripensamenti del progettista; la metodologia esposta deve in effetti costituire una linea di condotta dalla quale si può e si deve derogare con intuizioni o sguardi in avanti verso i livelli successivi e/o con ripensamenti o ritorni indietro verso i livelli di maggiore astrazione.
Progettare un programma per calcolare i primi N numeri primi.
Analisi del problema.
Per la risoluzione del problema si osserva che - per definizione - un numero j è primo se e solo se non è divisibile per alcuno dei numeri che lo precedono nella successione dei numeri naturali, da 2 a j-1; inoltre il numero 1 è primo. L'adozione di questa definizione come base per lo sviluppo dell'algoritmo richiederebbe che per ogni j vada provata la divisibilità per tutti i numeri precedenti.
Un'osservazione che consente di pervenire ad un algoritmo più efficiente è che "un numero è primo se non è divisibile per tutti i numeri primi ad esso inferiore". La maggiore efficienza dell'algoritmo dipende dal fatto che per ogni j andrà provata la divisibilità per un numero ben inferiore di divisori; per contro, tale decisione implica la necessità di memorizzare l'insieme di tutti i numeri primi via via trovati.
Il programma pertanto, al termine di questa fase di analisi può essere descritto al massimo livello di astrazione dall'istruzione seguente:
Calcola i primi N numeri primi.
Al secondo livello di astrazione del programma si può considerare che il blocco precedente si scomponga in tre blocchi:
immissione dei dati iniziali (input di N)
↓
elaborazione dei dati (calcolo dell'insieme dei primi N numeri primi)
↓
produzione del risultato (output dei numeri primi)
e contemporaneamente si assume la decisione che i dati intermedi, ottenuti a partire da quello iniziale vengano memorizzati in un array indicato con Primi. Le decisioni relative a operazioni di input e di output possono essere rinviate, concentrando l'attenzione sullo sviluppo del programma.
Il terzo passo del raffinamento consiste nello sviluppare il blocco "calcolo dell'insieme dei primi N numeri primi".
Coerentemente con l'analisi preliminare, si decide di calcolare nell'ordine gli N numeri primi e di adoperare a tale scopo un ciclo for con una variabile di controllo k.
|
|
 |
Al quarto livello di astrazione si decide di impiegare una variabile j che, partendo da un valore iniziale 0, si incrementa fino a quando diventa un numero primo da memorizzare nella posizione k dell'array Primi.
|
| 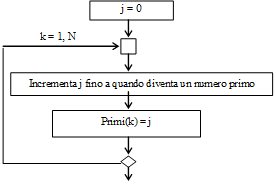 |
Nel quinto passo viene dettagliata la prima operazione interna al ciclo for, cioè il modo in cui j assume i valori:
|
Si deve osservare che non è necessario incrementare j di 1 perchè in questo modo j alternativamente diventa un numero pari e poi un numero dispari, e poichè di sicuro i numeri pari non sono primi si può inizializzare j con 3 e incrementarlo di 2. | 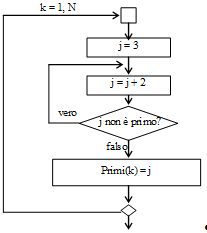 |
Al sesto passo si raffina il problema di determinare come realizzare la condizione "j non è primo", che comporta la ripetizione o la fine del ciclo.
Nell'analisi preliminare si è stabilito che j è primo se è 1, 2 oppure non è divisibile per alcuno dei numeri primi già trovati escluso l'1.
Se (j≠1 e j≠2) allora
se j non è divisibile per nessuno dei numeri primi minori di j
Allora j è primo
Altrimenti j non è primo
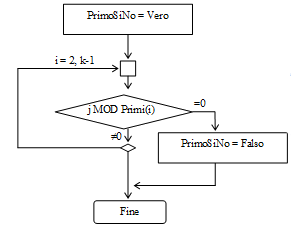
Il settimo passo descrive la soluzione del problema di stabilire se j è divisibile o no per i numeri primi minori di j: si tratta di dividere j per ciascuno dei k-1 numeri contenuti nell'array Primi.
Assegnare alla variabile logica PrimoSiNo il valore Vero
for(i=2; i<(k-1); i++)
(ripeti le operazioni seguenti dando alla variabile di controllo del ciclo i valori 2, 3, … k-1)
Se il resto della divisione tra j e Primi(i) è uguale a 0 allora
PrimoSiNo = Falso
interrompi il ciclo
Se il ciclo viene completato la variabile PrimoSiNo conserva il valore iniziale Vero.
Nella fase di ricostruzione del programma si possono apportare i seguenti miglioramenti:
Le posizioni Primi(1)=1 e Primi(2)=2 possono essere portate fuori dal ciclo in k, evitando così che per ogni valore di k si effettui il test j=1 o j=2; il ciclo in k dunque parte da 3.
Si possono provare per la divisibilità solo i numeri dispari (ciclo in j con valore iniziale 3 e incremento 2).
Anche il ciclo in i può iniziare da 3.
Altri raffinamenti, per evitare le operazioni inutili, possono essere: per provare la divisibilità si possono usare i numeri primi minori o uguali a j/2. O ancora si può provare la divisibilità per i numeri primi minori della radice quadrata di j.
Il test: j è primo?