Scratch

Lancio al Bersaglio

Si assume che il proiettile venga lanciato dall'origine degli assi del sistema di riferimento. Gli viene fornita una velocità iniziale V, inclinata rispetto al piano orizzontale di un angolo α.

Si vuole determinare

• la traiettoria del moto y(x),
• il tempo di volo,
• la distanza di caduta,
• la massima altezza raggiunta,

La velocità del proiettile è un vettore le cui componenti sono:

V_x = V·cos(α) (Componente lungo l'asse delle ascisse)
V_y = V·sen(α) (Componente lungo l'asse delle ordinate)

Traiettoria

La traiettoria percorsa dal proiettile può essere pensata che sia ottenuta dalla composizione di due moti:
Si immagini che il proiettile possegga solo la componente verticale della velocità. A questa bisogna sommare la velocità che il corpo acquista per effetto dell'accelerazione di gravità. Il moto verticale è quindi:

L'altra componente del moto può essere pensata che sia dovuta alla velocità V_x del sistema di riferimento che si muove nella direzione opposta. Il moto orizzontale, quindi, dovuto alla sola componente V_x è:

Ad agire contro la V_x ci potrebbe essere l'attrito dell'aria, ma lo si consideri nullo o trascurabile.

In altri termmini si ottiene lo stesso risultato se un osservatore si muove con velocità -V_x mentre il proiettile si muove solo lungo la verticale.

La traiettoria, quindi, viene determinata assegnando i corretti valori al tempo nelle due equazioni x(t) e y(t).

Tempo di volo

Per determinare i valori corretti da assegnare al tempo t, si deve conoscere qual è il tempo di volo, ovvero il tempo impiegato dal proiettile a raggiungere il suolo.

Per calcolare tale tempo bisogna imporre, nel moto verticale, che y sia pari all'altezza del punto di caduta. si assuma che il punto di partenza e il punto di arrivo si trovino allo stesso livello: y=0.

Si tratta quindi di risolvere l'equazione di secondo grado:

Che ammette due soluzioni, una coincide con il tempo di partenza e l'altra con il tempo di caduta

Si ottiene:

Gittata

Conoscendo il tempo di volo, si può calcolare la gittata, ovvero la distanza a cui cade il proiettile, calcolando lo spazio percorso in orizzontale dall'osservatore che nel sistema di riferimento si muove lungo la linea orizzontale, mentre il proiettile si muove lungo la verticale.

Massima altezza raggiunta.

Quando il proiettile raggiunge il punto più alto inverte la velocità, quindi nell'equazione del moto verticale, bisogna imporre V_y=0 e ricavare quindi il valore di t. Si trova che è metà del tempo di volo. Quindi l'altezza massima si ottiene:

---

Disegno della carta millimetrata

Nota: Questa sezione descrive il procedimento per disegnare la carta millimetrata. Se lo script è disponibile può essere importato dall'esercizio relativo alla carica del condensatore e quindi questa sezione può essere saltata e proseguire da quella successiva.

L'area dello stage ha 480 pixel in orizzontale e 360 pixel in verticale.

Si decide di posizionare l'origine degli assi nel punto di coordinate x=-200 e y=-150

Si elimini lo sprite del gatto e si prema il pulsante per creare un nuovo sprite. Comparirà l'editor di disegno, disegnare solo un punto, in una posizione qualsiasi e chiudere l'editor del disegno.

Lo sprite appena creato, verrà utilizzato per disegnare il reticolo di linee che rappresenta il foglio di carta millimetrata.

Algoritmo per disegnare gli assi cartesiani e la griglia millimetrata

1. Cancellare eventuali tracce presenti sullo stage
2. sollevare la penna
3. portarsi nell'origine degli assi
4. scegliere la penna di colore blu
5. abbassare la penna
6. (asse delle ascisse) muovere lo sprite in orizzontale fino a raggiungere il bordo destro dello stage
7. sollevare la penna
8. posizionarsi nell'origine degli assi
9. abbassare la penna
10. (asse delle ordinate) muovere lo sprite in verticale fino a raggiungere il bordo superiore dello stage.
11. Riportare lo sprite nell'origine degli assi.
12. algoritmo per tracciare la suddivisione dell'asse delle ascisse:
    ripeti le operazioni seguenti fino a quando la posizione x diventa > 220
    1. Alza la penna
    2. muovi lo sprite di 5 passi in orizzontale
    3. usa la penna di colore arancione
    4. se la posizione x è un multiplo di 25 usa la penna di colore rosso. (in questo modo ogni 5 linee di colore arancione se ne traccia una di colore rosso.
    5. abbassa la penna
    6. Traccia una linea verticale fino a raggiunere il bordo superiore dello stage.
    7. alza la penna
    8. ritorna sull'asse delle ascisse.

Codifica

• Dal menu Penna trascinare un blocco nell'area dello script.
• Dal menu Penna trascinare un blocco nell'area dello script.
• Si porti lo Sprite nel punto dove si è scelto di posizionare l'origine degli assi. Dal menu Movimento trascinare un blocco modificando la coordinata x in -200 e la coordinata y in -150.
• Trascinare un blocco scegliende il colore blu
• Dal menu Penna trascinare un blocco , per imporre la tracciatura del movimento dello Sprite.
• Disegnare la linea orizzontale corrispondente all'asse delle ascisse. Portare lo Sprite in posizione x=240 e y=-150. Trascinare un blocco modificando la coordinata x in 240.
• Per tracciare l'asse delle ordinate, si deve riportare lo Sprite nell'origine degli assi, ma prima si sollevi la penna:
• quindi portare lo sprite nell'origine: modificando la coordinata x in -200 e la coordinata y in -150.
• A questo punto abbassare la penna: trascinare un blocco
• Disegnare la linea verticale corrispondente all'asse delle ordinate. Trascinare un blocco modificando la coordinata y in 150.
• Sollevare la penna: e riportare lo sprite nell'origine degli assi: con x = -200 e y = -150.
• (direzione a destra)

Adesso si traccerà il reticolo di linee verticali, interponendo una linea di colore viola tra quattro linee di colore arancione.

Si sposterà lo sprite di 5 passi e si traccerà una linea. Quando lo sprite giunge in corrispondenza di un multiplo di 25 passi si cambia il colore della penna.

Si tracceranno linee, fintanto che la coordinata x dello sprite è minore di 220.

• Dal menu Controllo trascinare un blocco nell'area dello script.
• Nell'area incavata, trascinare un blocco
• nell'operando a sinistra del segno > trascinare il blocco:
• Nel secondo operando scrivere il valore 220, corrispondente al limite oltre terminare il disegno.
• all'interno del ciclo incastrare i seguenti blocchi:
  • 
  • , modificando il valore in 5 passi.
  • scegliendo il colore arancione.
  • Per cambiare colore della penna ogni 25 passi si usi un blocco SE, come il seguente:
    
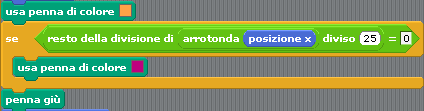
  • Incastrare un blocco per abbassare la penna.
  • Trascinare un blocco , modificando il valore in 150.
  • Sollevare la penna
  • Riportare lo Sprite sull'asse delle ascisse: e modificare il valore in -150.

Fino a questo punto si sono tracciate le linee verticali. Con un procedimento simile, che si mostra subito dopo, si devono tracciare le linee orizzontali.

• Sollevare la penna: e riportare lo sprite nell'origine degli assi: con x = -200 e y = -150.
• Fissare la direzione verso l'alto.
• Duplicare il blocco "Ripeti fino a quando" e incastrarlo sotto ai precedenti. Modificarlo come illustrato nella figura seguente.
  

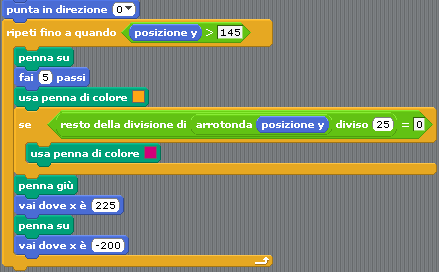
Eseguire lo Script

---

Disegnare la traiettoria

Importare lo Sprite della palla o, se si preferisce, disegnare un oggetto a proprio piacere, di dimensioni ridotte, che funga da proiettile

A questo nuovo sprite si associ lo script seguente:

• Nel menu Variabili, premendo il pulsante creare le seguenti variabili:
  • Dmax
  • Hmax
  • ScalaX
  • ScalaY
  • Tmax
  • Vel
  • Vx
  • Vy
  • alfa
  • t
  • x
  • y
• (facoltativo) Se lo sprite risulta troppo grande potrebbe convenire ridurne le misure: dal menu Aspetto trascinare un blocco e sostituire il 100 con 40 o con un valore che dia una dimensione più appropriata
• dal menu Sensori trascinare un blocco nell'area dello script, e sostituire il testo della domanda con il testo "Inserisci il modulo della velocità.
  Quando lo script verrà eseguito, accanto alla sprite comparirà la nuvoletta con dentro il testo della domanda e, sotto, una casella in cui viene mostrato il valore che si digita sulla tastiera.
  Quando si è terminato di scrivere il numero, premere il tasto Invio. Il valore viene mantenuto in un'area temporanea della memoria, in attesa di essere utilizzato.
• dal menu "Variabili" Trascinare un blocco e sostituire il nome della variabile con Vel. Nella casella contenente il valore 0 trascinare il blocco disponibile nel menu Aspetto. In questo modo il valore inserito da tastiera (Risposta), verrà memorizzato nella variabile Vel
• Portare un secondo blocco nell'area dello script, e sostituire il testo della domanda con il testo "Inserisci l'inclinazione della velocità.
• dal menu "Variabili" Trascinare un blocco e sostituire il nome della variabile con alfa. Nella casella contenente il valore 0 trascinare il blocco disponibile nel menu Aspetto.
• Calcolo delle componenti V_x e V_x della velocità:
  dal menu "Variabili" Trascinare un blocco e sostituire il nome della variabile con Vx. Nella casella riservata all'operando da scrivere nella variabile bisogna formare i blocchi che corrispondono alla moltiplicazione Vel*cos(α)
  Trascinare un blocco e inserirlo nel secondo operando del blocco "Porta variabile a...". Nella prima casella dell'operatore di moltiplicazione trascinare la variabile Vel. Nella seconda casella dell'operatore di moltiplicazione trascinare un blocco e selezionare la funzione cos. Portare la variabile alfa nella casella dell'operando della funzione coseno.
• Ripetere le stesse operazioni del passo precedente per costruire l'espressione V_y = Vel*sin(α).
  
• Calcolo del tempo di volo: t_max = 2·V_x/g:
  
  Dal menu Variabili trascinare un blocco "Porta (variabile) a ..." e sostituire il nome della variabile con la variabile Tmax. Nella casella dell'operando comporre l'espressione 2*Vy/9,81, usando un blocco e un blocco :
  
• Calcolo della gittata. Conoscendo il tempo di volo si calcola il punto di caduta. D = V_x·t_max
  
  
• Calcolo della massima altezza raggiunta: Hmax = V_y··(Tmax/2) - ½·9.81·(Tmax/2)²
  
  Attenzione alla precedenza tra gli operatori: Trascinare prima un blocco e completare i due operandi secondo le operazioni indicate nell'espressione del calcolo.
  
  Essendo l'espressione piuttosto lunga è facile incorrere in errori, quindi conviene scriverla calcolando prima (Tmax/2)², memorizzando il risultato nella variabile Hmax.
  poi moltiplicare tale variabile per 9.81, dividere il risultato per 2 e memorizzare il risultato in Hmax.
  Infine calcolare V_y·(Tmax/2), sottrarre il valore contenuto in Hmax e memorizzare il risultato in Hmax.
  
• Usando due blocchi Assegnare i corretti valori alle due variabili ScalaX e ScalaY:
  
  ScalaX = 480/40
  ScalaY = 320/8
  Nota: i valori scelti danno a una traiettoria che rientra completamente all'interno dello stage se si assegna la velocità iniziale = 20 m/s e l'inclinazione = 30°.
• Assegnare il valore 0 alla variabile t
• Sollevare la penna
• muovere lo sprite nell'origine degli assi.
• Abbassare la penna
• scegliere la penna di un colore non ancora usato, ad esempio verde scuro.
• Dal menu Controllo trascinare un blocco
• Nella parte incavata del blocco Repeat ... Until ... inserire un blocco di confronto:
• Nell'operando di sinistra del blocco di confronto inserire il blocco e nell'operando di destra scrivere il valore -150, ovvero: quando la palla tocca l'asse delle ascisse si termina il procedimento di calcolo della traiettoria.
• All'interno del blocco Repeat ... Until ... inserire i seguenti blocchi:
  • incrementare t della quantità Δt=R*C/100:
    
  • Calcolare il valore dell'altezza y:
    
  • calcolare la posizione orizzontale:
    
  • Portare lo sprite nella nuova posizione:
    

Collaudo

Dopo aver verificato il funzionamento del programma con vari valori di input individuare i comportamenti errati del programma ed introdurre gli opportuni controlli:
- quando lo sprite esce dallo stage sollevare la penna,
- non accettare valori di input esterni ad un determianto intervallo.