CAMBIA STILE

CAMBIA TEXTURE

CAMBIA COLORE

CALCOLO



TEORIA DEI CAMPIONI

Per lo studio di un fenomeno non è sempre possibile eseguire una rilevazione sull'intera popolazione statistica, ma spesso si può disporre solo di un insieme di unità statistiche che costituiscono un campione. Quando si estendono alla popolazione i risultati ottenuti dal campione, si dice che si opera un'inferenza statica. L'inferenza statistica è, quindi, una branca della statistica che studia i campioni e la loro scelta.

Ci sono varie ragioni per cui preferire un'indagine campionaria, quali:

  • - Indagine più approfondita su una parte dell'universo;
  • - Notevole risparmio dei costi;
  • - Notevole risparmio di tempo.

COSTRUZIONE DEL CAMPIONE

La procedura standard parte da dati Istat, facendo in modo che all'interno del campione siano rappresentate nei corretti rapporti tutte le fasce sociali e demografiche: sesso, età, grado di istruzione, residenza, lavoro, reddito. Se il sondaggio lo richiede, si possono considerare altri elementi (statura, peso, sport praticato, alimentazione). Il campione può essere rappresentativo non solo di chi vive in una Regione o uno Stato, ma anche di una categoria: lavoratori dipendenti, avvocati, gelatai, ecc.


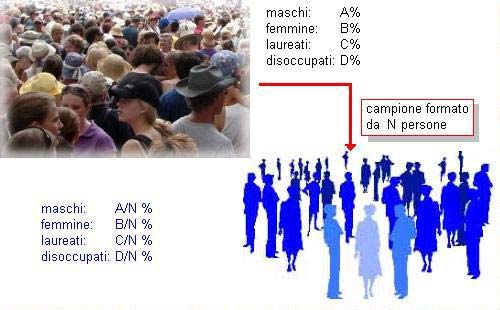
Esempio: posto che in Italia, il 5% della popolazione è laureato, allora un campione di 100 persone dovrà comprendere 5 laureati; le altre classi costitutive saranno presenti seguendo lo stesso criterio.

IL CAMPIONAMENTO CASUALE SEMPLICE

Il problema fondamentale di una rilevazione campionaria è la scelta del campione rappresentativo della popolazione. Il metodo più importante per la scelta di un campione è il campionamento casuale semplice, in cui la scelta è affidata al caso e chi compie l'indagine non deve influenzare la scelta.

Vantaggi:

  • 1) E' il tipo di campionamento più semplice che consente di fare riferimento ai modelli più elementari di calcolo delle probabilità;
  • 2) Richiede una minima conoscenza a priori delle caratteristiche della popolazione;
  • 3) Le stime dei parametri della popolazione e dei loro errori medi sono molto facili;
  • 4) E' particolarmente conveniente quando la popolazione non è molto grande.

Svantaggi:

  • 1) Comporta spesso costi di rilevazione più elevati rispetto ad altri procedimenti di scelta delle unità campionarie;
  • 2) A parità di dimensione, ossia del numero di osservazioni, può condurre a stime dei parametri della popolazione meno precise di quelle ottenute con altri tipi di campionamento;
  • Nella pratica non viene molto impiegato, poiché la maggioranza delle indagini agisce su grandi dimensioni;

Le caratteristiche del campionamento casuale semplice sono:

  • 1) tutte le unità della popolazione possono far parte del campione;
  • 2) ogni campione di ampiezza n ha la stessa probabilità di essere formato.

La scelta di un campione casuale semplice di n elementi può essere fatta secondo due tipi di estrazioni:

  • a) Estrazione bernoulliana (o con ripetizione), si calcola come disposizioni con ripetizioni di N elementi di classe n, cioè:
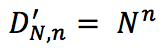
  • b) Estrazione in blocco (o senza ripetizione), che si calcola come numero delle combinazioni semplici di N elementi di classe n, cioè:
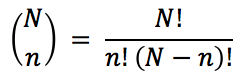
  • L'insieme dei campioni viene detto spazio dei campioni, mentre il rapporto 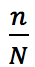fra l'ampiezza del campione e il numero delle unità della popolazione, è detto tasso di campionamento.

PARAMETRI E STIMATORI

Nello studio di un carattere di una popolazione statistica si cerca di sinterizzare i vari dati con un valore caratteristico come un valore medio, un indice di variabilità, una frequenza ecc…

Si definisce parametro di una popolazione un valore caratteristico della popolazione, mentre si definisce stimatore del parametro quel valore caratteristico dell'universo.

ERRORE DI CAMPIONAMENTO

Il fattore responsabile della generazione di un errore di campionamento è riconducibile alla variazione casuale, cioè ad un insieme di cause, piccole o grandi, che agiscono imprevedibilmente su un fenomeno senza che noi possiamo contrastarne l'azione. L'errore di campionamento non può mai essere determinato con esattezza.

Esempio: il campione prelevato con una biopsia epatica rappresenta circa 1/50000 dell'organo. Essendo il campione così piccolo rispetto all'intero organo, è possibile che l'intero organo sia ammalato, ma proprio quel campione prelevato sia sano. A questo punto si verificherebbe un errore di campionamento, poiché il dottore diagnosticherebbe sano l'intero organo basandosi su quel campione.

CAMPIONAMENTO PER STRATIFICAZIONE

Un altro tipo di campionamento è quello per stratificazione. Il primo passo da compiere è la suddivisione della popolazione, dalla quale si intende estrarre il campione, in sottopopolazioni dette "strati", il più possibile omogenei rispetto alla variabile di cui si intende stimare il valore. Successivamente si estrae, mediante una procedura di campionamento casuale semplice, il campione relativo a ciascuno strato, ed infine si uniscono tali campioni, ottenendo in questo modo il campione globale.

Vantaggio:

  • 1) Maggiore rappresentatività del campione;

Svantaggi:

  • 1) Se non si hanno sufficienti informazioni a priori, la costruzione degli strati può risultare alquanto costosa;
  • 2) Se la stratificazione è errata si ottengono risultati fuorvianti.

CAMPIONAMENTO A GRAPPOLI

Il campionamento a grappoli è un tipo di campionamento che non prevede l'estrazione di un singolo individuo come rappresentante della popolazione, ma di grappoli di individui con tutte le unità "appartenenti" al grappolo. Ad esempio, classi scolastiche, reparti di lavoro o camere di ospedale vengono chiamati "grappoli", e inclusi nel campione.

CAMPIONAMENTO A PIÙ STADI

È una tecnica di campionamento che risulta molto vantaggiosa quando la popolazione da studiare è molto numerosa e gli elementi possono essere raggruppati in diversi sottoinsiemi. È economicamente e temporaneamente vantaggioso, ma la stima è imprecisa.
Dopo aver suddiviso la popolazione di partenza in successive sottoclassi o stadi (es. province, comuni, scuole e così via), si estrae un campione di unità di primo stadio (province) e nell'ambito delle unità ottenute si procede alla scelta dei campione di secondo stadio (comuni) e cosi via. Il campione è costituito dalle unità estratte dall'ultimo stadio.
Questa tecnica viene spesso utilizzata, ad esempio, nei sondaggi di opinione.

CAMPIONAMENTO SISTEMATICO

E' una tecnica di campionamento con la quale si tiene sotto controllo la produzione. Si elencano tutte le unità statistiche della popolazione e, partendo dalla prima unità scelta a caso, si estrae un’unità ogni k unità.

CAMPIONAMENTO NON PROBABILISTICO

Non permette di stimare l’errore probabile. Si suddivide in:

  • 1) Campionamento ragionato: ottenuto su suggerimento di esperti; Questo campione potrebbe anche essere rappresentativo, ma non esiste un criterio per misurare il grado di fiducia.
  • 2) Campionamento per quote: gli elementi del campione vengono scelti secondo il sesso, l’età, lo stato sociale ecc.. Si è dimostrato che il campionamento cosi formato è un campionamento distorto.